今回は、大学入試制度の解説の続編となります。
前回解説をした大学入学共通テストについて,教科ごとにみていきます。
まずは、数学です。
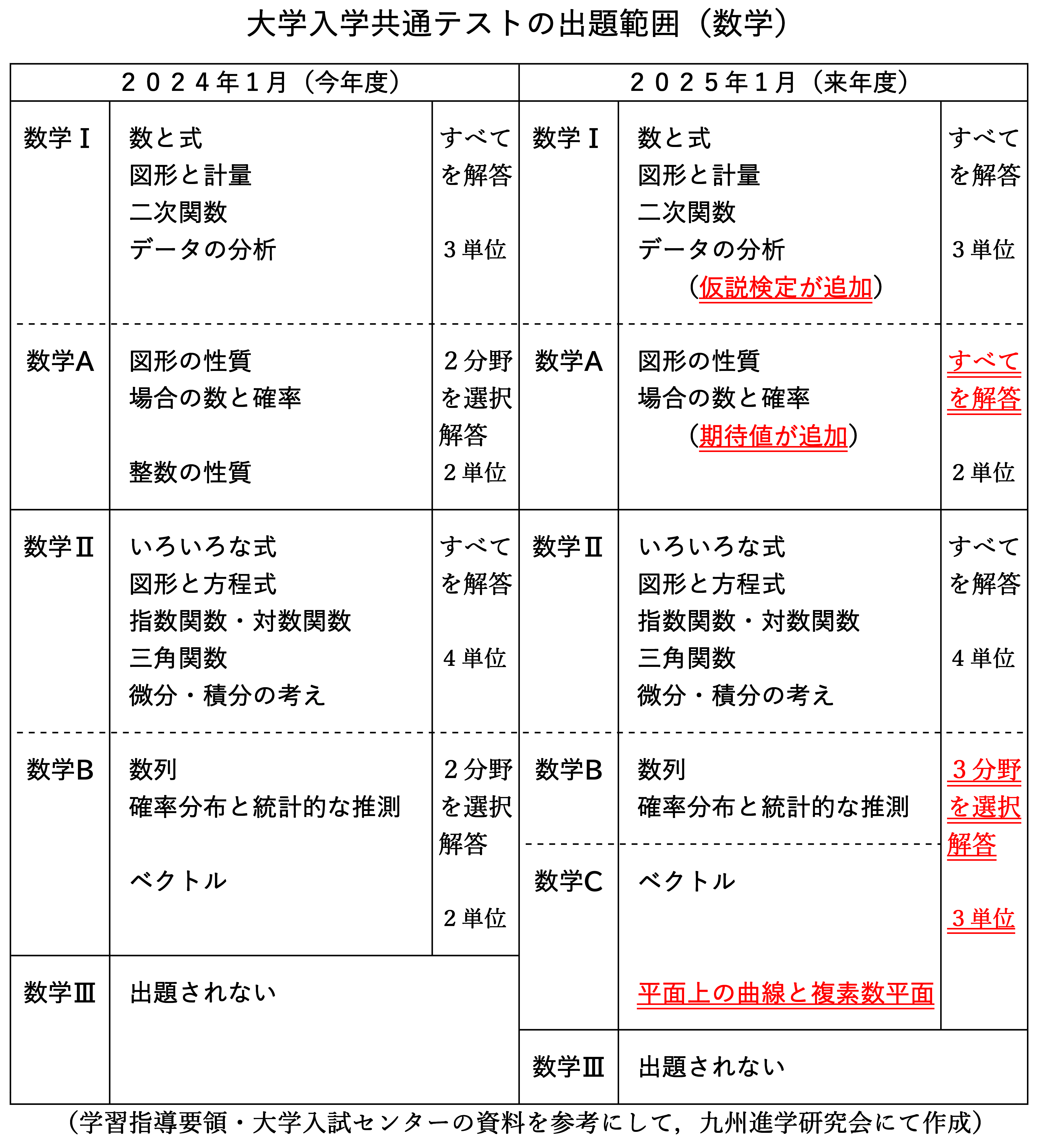
赤字下線部が変更点です。
表中の「単位」とは学習量を示しており,35時間✕単位数が学習量となります。
おおよそ「1週の授業時間✕年」に相当すると理解すれば良いでしょう。
例えば,4単位は「1週に4時間授業で1年間」や「1週に8時間授業で半年」などとなります。
まず,3年生になったら本気出すなどの考えが甘いということを理解してください。
共通テストの試験範囲は合計で12単位,すなわち420時間分の学習となります。
これを3年生になってからの9ヶ月(共通テストは1月ですので,4~12月)で入試対策を含めて終わらせる自信や覚悟がありますか?
入試は1教科だけではないことを忘れていませんか?
さて,試験範囲をみると,量・質ともに無視できないレベルで増加していることがわかります。
① 数学Ⅰ+A
用語(定理公式)の追加があります。
いずれも旧課程の数学B(確率分布と統計的な推測)で学習していた内容です。
「確率分布と統計的な推測」は,旧課程まではほとんど授業が行われていませんでした。
そのため,高校(数学教員)にもノウハウがほとんどありません。
また,数学Aで選択が廃止されます。
このことにより「苦手分野から逃げられない」ことになります。
② 数学Ⅱ+B+C
数学Ⅱは変化ありません。
しかし,数学Cの追加により試験範囲が単元レベルで増加します。
試験時間が10分延長(70分)されるのは,このためだと思われます。
これが前回の解説での「教科書換算で60~80ページ程度」のことです。
1単位分の増加,すなわち「週2時間授業で半年」という学習量ですので,教科書の終了が遅い時期にずれ込むことになります。
受験勉強で使える時間に影響することは言うまでもありません。
また,学習が大変な内容でもあります。
旧課程では「数列+ベクトル」を選択することが標準的だったのですが,次回からはあと1分野の選択が必要となります。
「確率分布と統計的な推測」または「平面上の曲線と複素数平面」です。
「確率分布と統計的な推測」は①に書いたように,これまで授業が行われていませんでした。
「平面上の曲線と複素数平面」は旧課程の数学Ⅲ(いわゆる、理系数学)の学習内容です。
どちらを選ぶにしても大変なことになります。(数学の教員はどちらの授業をするか悩んでいたらしいです。)
理系生徒は「平面上の曲線と複素数平面」を選択すれば良いのでしょうが,旧課程では二次対策のみでよかったのが共通テスト対策もする必要がでてきましたので,影響がないわけではありません。
